Ohmin laki koko ketjulle ja ketjun osalle: vaihtoehdot kaavan, kuvauksen ja selityksen kirjoittamiseen

Ammattimainen sähköasentaja tai elektroniikkaasiantuntija ei voi ohittaa Ohmin lakia omassa toiminnassaan ratkaisemalla elektronisten ja sähköisten piirien asennukseen, säätöön ja korjaamiseen liittyviä ongelmia.

Itse asiassa kaikkien on ymmärrettävä tämä laki. Koska jokainen joutuu käsittelemään sähköä jokapäiväisessä elämässä.

Ja vaikka saksalainen fyysikko Ohmin laki on säädetty lukion opetussuunnitelmassa, käytännössä sitä ei aina opiskella ajoissa. Siksi materiaalissamme tarkastelemme niin merkityksellistä elämän aihetta ja ymmärrämme kaavan kirjoittamisen vaihtoehdot.

Yksiosainen ja täydellinen sähköpiiri

Kun tarkastellaan sähköpiiriä Ohmin lain soveltamisen kannalta piiriin, tulee huomioida kaksi mahdollista laskentavaihtoehtoa: erilliselle osalle ja täysimittaiselle piirille.

Sähköpiirin osan virran laskenta

Sähköpiirin osan katsotaan yleensä olevan se piirin osa, joka sulkee pois EMF-lähteen, koska sillä on ylimääräinen sisäinen vastus.

Siksi laskentakaava näyttää tässä tapauksessa yksinkertaiselta:

I = U/R,

Missä vastaavasti:

• minä – virran voimakkuus;
• U – käytetty jännite;
• R - vastustuskyky.

Kaavan tulkinta on yksinkertainen - piirin tietyn osan läpi kulkeva virta on verrannollinen siihen syötettyyn jännitteeseen ja vastus on kääntäen verrannollinen.

Niin kutsuttu graafinen "päiväkakkara", jonka kautta esitetään koko joukko Ohmin lakiin perustuvia formulaatioiden muunnelmia. Kätevä työkalu taskuvarastoon: sektori "P" - tehokaavat; sektori "U" - jännitekaavat; sektori "I" - nykyiset kaavat; sektori "R" - vastuskaavat

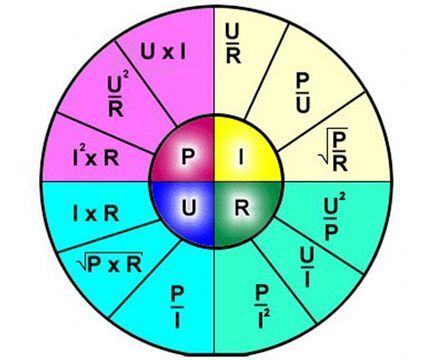
Siten kaava kuvaa selvästi virran riippuvuuden sähköpiirin erillisen osan läpi suhteessa tiettyihin jännitteen ja vastuksen arvoihin.

Kaavaa on kätevä käyttää esimerkiksi laskettaessa piiriin juotettavan resistanssin parametreja, jos jännite ja virta on annettu.

Ohmin laki ja kaksi seurausta, jotka jokaisen ammattimaisen sähkömekaanisen insinöörin, sähköinsinöörin, elektroniikkainsinöörin ja kaikkien sähköpiirien käyttöön osallistuvien on tiedettävä. Vasemmalta oikealle: 1 - virran määritys; 2 - vastuksen määrittäminen; 3 - jännitteen määritelmä, jossa I - virta, U - jännite, R - vastus

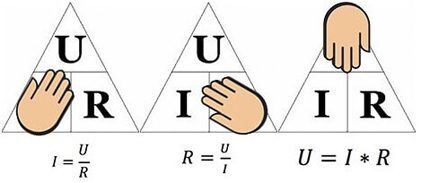
Yllä oleva kuva auttaa määrittämään esimerkiksi 10 ohmin resistanssin läpi kulkevan virran, johon syötetään 12 voltin jännite. Arvot korvaamalla saadaan – I = 12 / 10 = 1,2 ampeeria.

Resistanssin (kun virta ja jännite tunnetaan) tai jännitteen (kun jännite ja virta tunnetaan) löytämisen ongelmat ratkaistaan ​​samalla tavalla.

Siten voit aina valita tarvittavan käyttöjännitteen, vaaditun virranvoimakkuuden ja optimaalisen resistanssielementin.

Käytettäväksi ehdotettu kaava ei vaadi jännitelähteen parametrien huomioon ottamista.Kuitenkin piiri, joka sisältää esimerkiksi akun, lasketaan eri kaavalla. Kaaviossa: A – ampeerimittarin kytkeminen päälle; V – kytke volttimittari päälle.

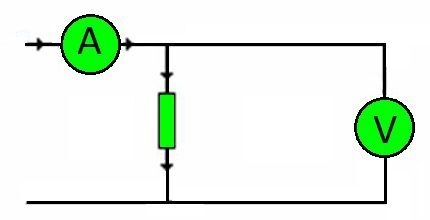
Muuten, minkä tahansa piirin liitäntäjohdot ovat vastuksia. Niiden kantama kuormitus määräytyy jännitteen mukaan.

Näin ollen, jälleen Ohmin lakia käyttäen, on mahdollista valita tarkasti tarvittava johtimen poikkileikkaus ydinmateriaalista riippuen.

Meillä on tarkat ohjeet verkkosivuillamme kaapelin poikkileikkauksen laskeminen tehon ja virran suhteen.

Koko ketjun laskentavaihtoehto

Täydellinen piiri koostuu osasta (osista) sekä EMF-lähteestä. Eli itse asiassa EMF-lähteen sisäinen resistanssi lisätään piiriosan olemassa olevaan resistiiviseen komponenttiin.

Siksi on loogista muuttaa hieman yllä olevaa kaavaa:

I = U / (R + r)

Tietysti EMF:n sisäisen resistanssin arvoa Ohmin laissa täydelliselle sähköpiirille voidaan pitää merkityksettömänä, vaikka tämä vastusarvo riippuu suurelta osin EMF-lähteen rakenteesta.

Kuitenkin laskettaessa monimutkaisia ​​elektronisia piirejä, sähköpiirejä, joissa on monia johtimia, lisävastuksen läsnäolo on tärkeä tekijä.

Tehtäessä laskelmia täydellisen sähköpiirin olosuhteissa EMF-lähteen resistiivinen arvo otetaan aina huomioon. Tämä arvo summataan itse sähköpiirin resistiivisellä resistanssilla. Kaaviossa: I - virtaus; R - ulkoinen resistiivinen elementti; r on EMF:n (energialähteen) resistiivinen tekijä

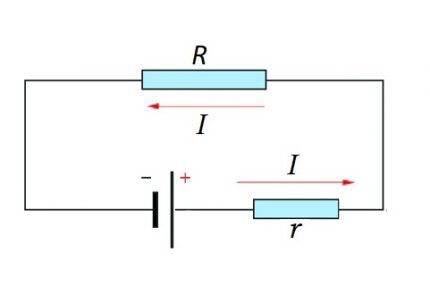
Sekä piirin osissa että koko piirissä tulee ottaa huomioon luonnollinen momentti - vakio- tai muuttuvavirran käyttö.

Jos edellä mainitut Ohmin laille ominaiset kohdat tarkasteltiin tasavirran käytön kannalta, niin vaihtovirralla kaikki näyttää hieman erilaiselta.

Lain vaikutuksen huomioon ottaminen muuttuvaan suureen

Käsitettä "vastus" kulkevan vaihtovirran olosuhteille tulisi pitää enemmän kuin "impedanssin" käsitettä. Tämä viittaa resistiivisen kuorman (Ra) ja reaktiivisen vastuskuorman (Rr) yhdistelmään.

Sellaiset ilmiöt johtuvat induktiivisten elementtien parametreista ja kytkentälaeista suhteessa muuttuvaan jännitearvoon - sinimuotoiseen virran arvoon.

Tämä on vaihtovirtasähköpiirin vastaava piiri laskettaessa Ohmin lain periaatteisiin perustuvia formulaatioita: R - resistiivinen komponentti; C on kapasitiivinen komponentti; L-induktiivinen komponentti; EMF on energianlähde; I - virta

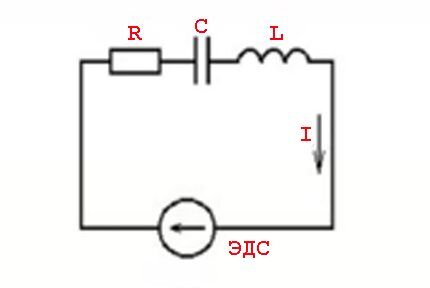
Toisin sanoen jännitearvoista johtavien (lag) virta-arvojen vaikutus, johon liittyy aktiivisten (resistiivisten) ja reaktiivisten (induktiivisten tai kapasitiivisten) tehojen ilmaantumista.

Tällaiset ilmiöt lasketaan kaavalla:

Z=U/I tai Z = R + J* (X_L -X_C)

Missä: Z – impedanssi; R – aktiivinen kuorma; X_L , X_C – induktiivinen ja kapasitiivinen kuorma; J - kerroin.

Elementtien sarja- ja rinnakkaiskytkentä

Sähköpiirin elementtien (piirin osan) ominaispiste on sarja- tai rinnakkaiskytkentä.

Vastaavasti jokaiseen liitäntätyyppiin liittyy erilainen virta- ja jännitteensyöttökuvio.Tässä suhteessa Ohmin lakia sovelletaan myös eri tavalla elementtien sisällyttämisvaihtoehdon mukaan.

Sarjaan kytkettyjen resistiivisten elementtien piiri

Sarjakytkennässä (piirin osa, jossa on kaksi komponenttia) käytetään seuraavaa muotoilua:

• minä = minä₁ = minä₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Tämä muotoilu osoittaa selvästi, että riippumatta sarjaan kytkettyjen resistiivisten komponenttien lukumäärästä, piirin osan läpi kulkeva virta ei muutu arvossaan.

Resistiivisten elementtien kytkentä piirin osassa sarjaan keskenään. Tällä vaihtoehdolla on oma laskentalakinsa. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U, U1, U2 - syötetty jännite

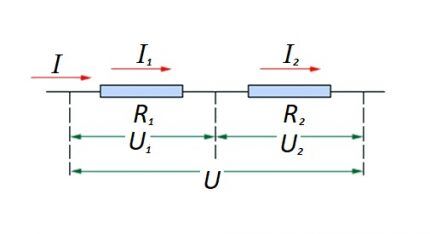
Piirin tehollisille resistiivisille komponenteille syötetyn jännitteen suuruus on summa ja summaa emf-lähteen arvon.

Tässä tapauksessa kunkin yksittäisen komponentin jännite on yhtä suuri: Ux = I * Rx.

Kokonaisvastusta tulisi pitää kaikkien piirin resistiivisten komponenttien arvojen summana.

Rinnakkaisten resistiivisten elementtien piiri

Siinä tapauksessa, että resistiiviset komponentit on kytketty rinnakkain, seuraavaa muotoilua pidetään oikeudenmukaisena suhteessa saksalaisen fyysikon Ohmin lakiin:

• minä = minä₁ +I₂ … ;
• U = U₁ =U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Vaihtoehtoja "sekatyyppisten" piiriosien luomiseksi, kun käytetään rinnakkais- ja sarjaliitäntöjä, ei suljeta pois.

Resistiivisten elementtien kytkentä piirin osassa rinnakkain. Tässä vaihtoehdossa sovelletaan erilaista laskentalakia. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U on syötetty jännite; A, B - tulo-/poistumispisteet

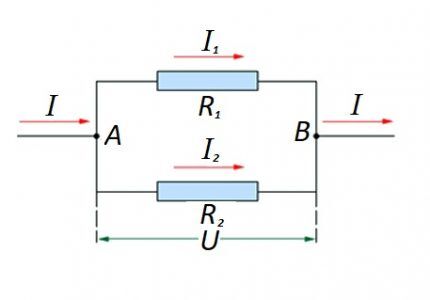
Tällaisille vaihtoehdoille laskenta suoritetaan yleensä laskemalla aluksi rinnakkaisliitännän resistiivinen arvo. Sitten saatuun tulokseen lisätään sarjaan kytketyn vastuksen arvo.

Lain integraaliset ja differentiaaliset muodot

Kaikki yllä olevat kohdat laskelmilla ovat sovellettavissa olosuhteisiin, joissa sähköpiireissä käytetään niin sanotusti "homogeenisen" rakenteen johtimia.

Samaan aikaan käytännössä joutuu usein tekemisiin kaavioiden rakentamisen kanssa, jossa johtimien rakenne muuttuu eri osissa. Esimerkiksi käytetään suuremman poikkileikkauksen omaavia tai päinvastoin pienempiä lankoja, jotka on valmistettu eri materiaaleista.

Tällaisten erojen huomioon ottamiseksi on olemassa muunnelma niin sanotusta "differentiaali-integraali Ohmin laista". Äärettömän pienelle johtimelle virrantiheystaso lasketaan jännitteen ja johtavuusarvon mukaan.

Differentiaalilaskennassa käytetään seuraavaa kaavaa: J = ό * E

Vastaavasti integraalilaskelman muotoilu on: I * R = φ1 – φ2 + έ

Nämä esimerkit ovat kuitenkin melko lähempänä korkeamman matematiikan koulukuntaa, eikä niitä varsinaisesti käytetä yksinkertaisen sähköasentajan todellisessa käytännössä.

Päätelmät ja hyödyllinen video aiheesta

Ohmin lain yksityiskohtainen analyysi alla olevassa videossa auttaa lopulta vahvistamaan tietämystä tähän suuntaan.

Ainutlaatuinen videotunti vahvistaa laadullisesti teoreettista kirjallista esitystä:

Sähköasentajan työ tai elektroniikkainsinöörin toiminta liittyy kiinteästi hetkiin, jolloin Georg Ohmin lakia on todella tarkkailtava toiminnassa. Nämä ovat eräänlaisia ​​totuuksia, jotka jokaisen ammattilaisen tulisi tietää.

Laajaa tietämystä tästä aiheesta ei vaadita - riittää, että oppii sanamuodon kolme päämuunnelmaa, jotta sitä voidaan soveltaa menestyksekkäästi käytännössä.

Haluatko täydentää yllä olevaa materiaalia arvokkailla kommenteilla tai ilmaista mielipiteesi? Kirjoita kommentit artikkelin alla olevaan lohkoon. Jos sinulla on kysyttävää, älä epäröi kysyä asiantuntijoiltamme.